Determining the Domain of a Rational Function & the Zen of Bouncing
Project Info
- Written by Kelvin Holland
- Category Writing, Curriculum & Education:Precalculus
Determining the Domain of a Rational Function & The Zen of Bouncing
Today, we are going to learn how to find the domain of a function. In the previous modules, we learned that domain is the term for the set of x values or inputs for a function. Range is the term for the set of y values or the output of a function.
If we look at the linear equation f(x) = 3x + 2, the domain would be all real numbers. The reason for this is that you can insert any real number for the value of x in f(x) = 3x + 2 and the function will produce a value for y. But not every function is as straightforward as a line (pun intended). There are some functions (e.g., rational equations, radical equations) for which certain values for x cannot be used because the function cannot produce a value for y from the input. These sort of x values are outside the domain. Then where do you begin? What do you do? Let’s begin with a personal anecdote.
A long time ago, before I had my current physique of Kung-Fu Panda (after the Jurassic Period but before Xbox One), I was young and athletic. And for a short while, I was a bouncer at a sports bar called Mulligan’s. One of the responsibilities of the bouncer is to determine who can legally enter the establishment. I’m going to show you what being a bouncer has in common with finding the domain of a function.
I want you to use your imagination and imagine a night club. But this is not your ordinary night club. This is a math night club. The name of the math night club is Club Domain. Its slogan is “there ain’t no party like a math party cuz a math party don’t stop.”

But instead of the club featuring a different genre of music each night of the week, it features a different function.
Let’s say it is Friday night, and the function featured that night is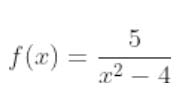
You are the new bouncer at Club Domain, so you have to work the door. Numbers are standing in line to get into Club Domain. As the bouncer at Club Domain, you have to determine which numbers are valid or legal, so to speak, to enter the club.
So, you are going to be on the lookout for troublemakers trying to get in the club. There are two types of troublemakers, and they are easy to spot.
First Troublemaker
Any number for x that makes an entire denominator equal to 0.
Why? Because you cannot divide by 0. It is undefined. Taboo numero uno!
Second Troublemaker
Any number for x that makes quantity inside of an even radical equal to a negative number.
Why? Because the even root of a negative number is called an imaginary number. We cannot use this type of coordinate plane to graph an imaginary number.
Let’s return to our original scenario. It’s Friday night, and the club is jumping to the following function: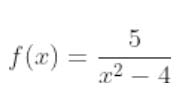
Can you identify which of the two troublemakers types should give you the most concern?
First Troublemaker type is the correct answer. Our function is a rational function, a rational function has a denominator.
Can you determine which number(s) cannot be let into the club?
Let’s ID (determine the domain status) of the first number in line: -3. We plug -3 into x and f(x) gives us 1. Looks good. Let’s see it on the graph. Still looks good. You can let -3 into the club.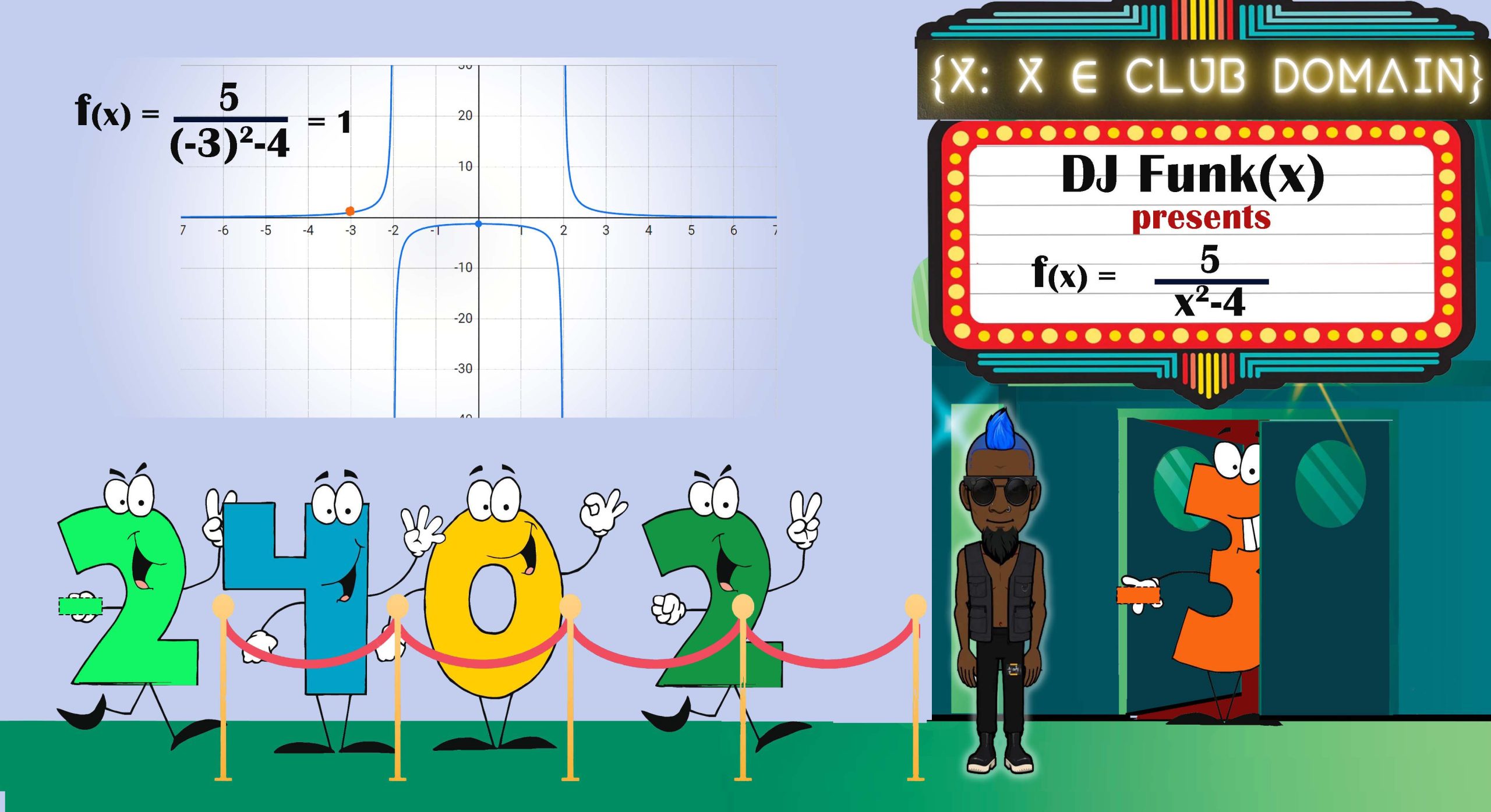
Let’s ID (determine the domain status) of the second number in line: 2. When we plug the value of 2 for x, the function is undefined. There is no corresponding y value. What we have is a gap called a vertical asymptote. You can think of it as an invisible fence that the graph can never touch. The graphed function will get infinitesimally close to 2, but never ever touch it.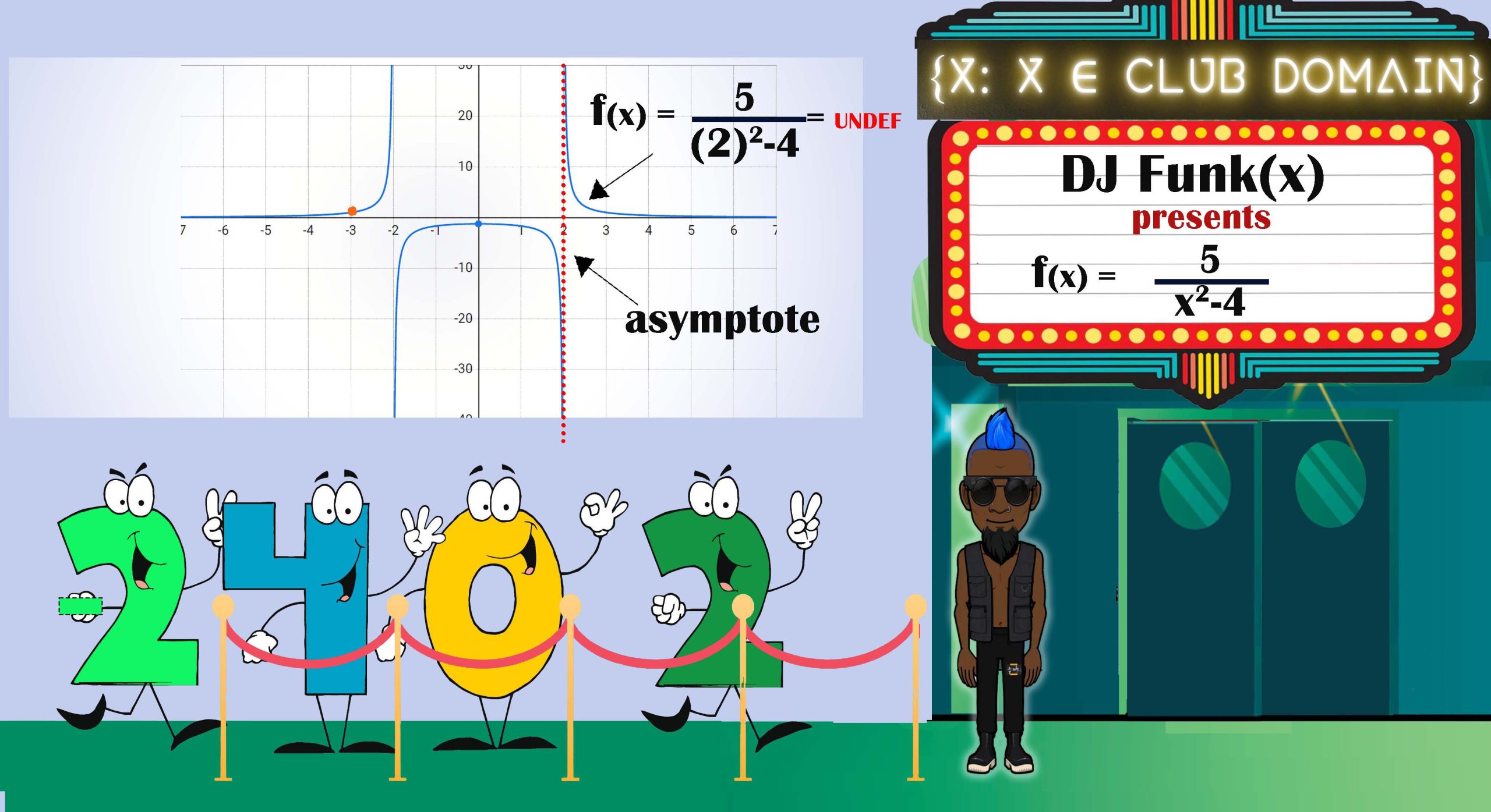
Can you ID the other numbers in line? Is there any other number we cannot let into the club?
If you said -2, you are correct. The value 2 is on a vertical asymptote.
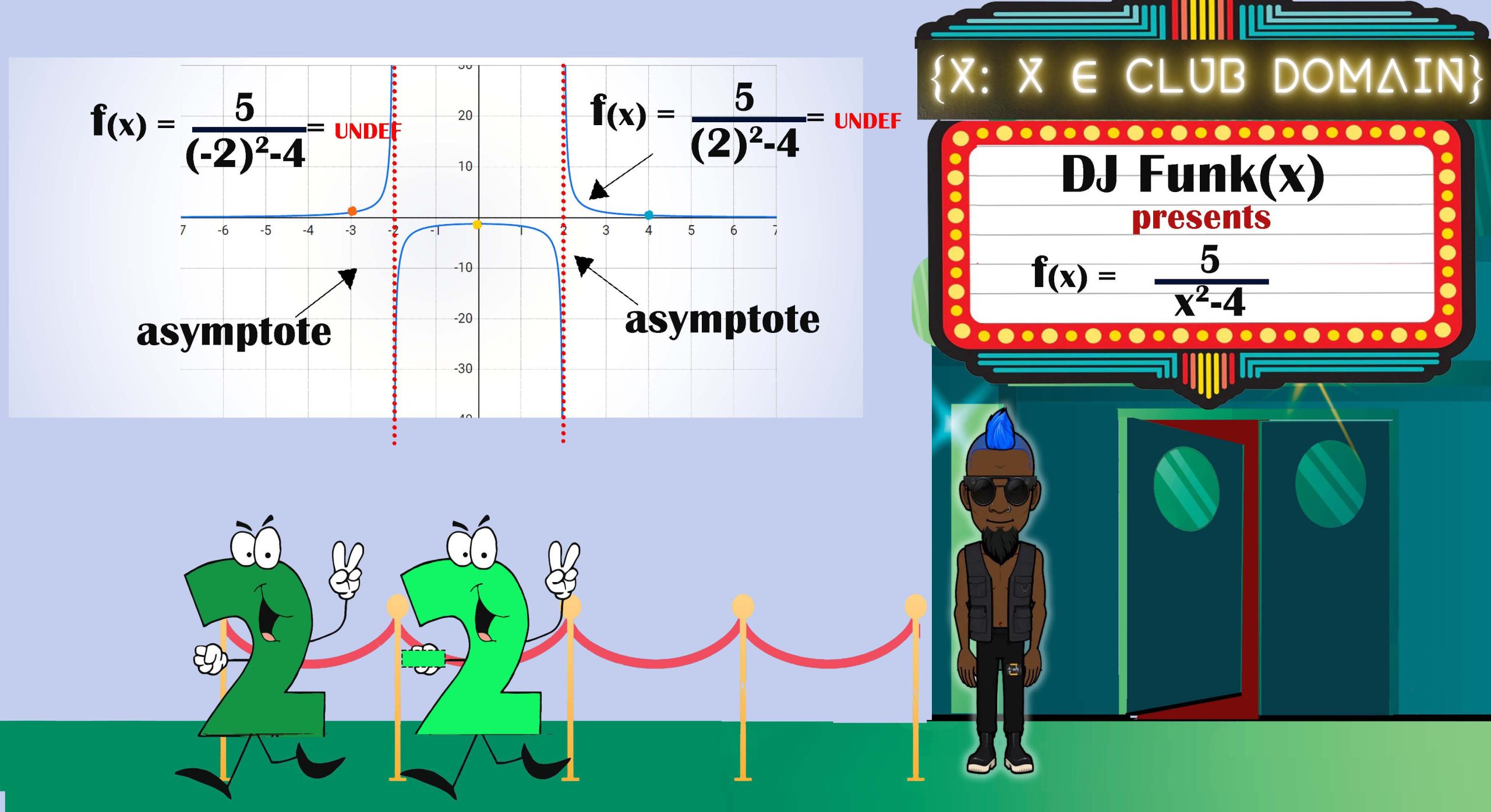
So for the function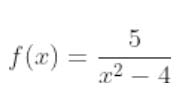
our domain is all real numbers except -2 and 2.
I hope you have a better grasp of how to determine the domain of a function now.
There’s just one more thing. If -2 and 2 try to give you a hard time for not letting them in the club, what should you say to them?
Correct Answer: Tonight’s not your night. Beat It!
Don’t make me have to kick your asymptotes!
